7 Histogramas :D

GRÁFICOS DE CONTROL

Unidad 4. Funciones Matemáticas :)

Explica la diferencia entre un escalar y un vector.

Magnitud, dirección y sentido es vectorial, mientras que escalar solo tiene magnitud. Ejemplo: La fuerza es vectorial, mientras que la masa es escalar.

Anota tres ejemplos de cada uno.

Vector: Velocidad, unidad y fuerza. 

Escalar: Masa, tiempo y longitud.

Ejemplo de Escalar:

12kg, 5m, 70km/h, las cantidades escalares se pueden sumar, restarse, con la condición que sean de su misma especie. 

Ejemplo: 14kg + 10kg = 24kg

Cantidad Escalar: Es aquella la cual se especifica por su magnitud  y unidad o especie.

Explica el concepto de vector unitario.

Es un vector sin dimensiones que tiene una magnitud de exactamente uno (1). Los vectores unitarios se usan para especificar una dirección conocida y no tienen otro significado físico. Se usaran los símbolos i, j, k, para representar los vectores unitarios que apuntan a las direcciones x, y  z.

Efectúa las siguientes operaciones con los vectores indicados.

Operaciones

a) a+b+c

b)a-b

c)a-c

d)axb

e)a*b

(5i+8j+3k)

(-8i+6j-3k)

(3i-8j-7k)

5	-8	3
		3
8	6	-3
		11
3	-8	-7
		-12

= 3i + 11j -12k

B= (5i +8j + 3k) – (-8i +6j -3k)

40i – 48j +9k

C= (5i +8j + 3k) - (3i-8j-7k)

 -15i + 64j + 21k

D= (5i +8j + 3k) x (-8i +6j -3k)

(5i) (-8i) = -40i (8j) (6j) =48j  (3k) (-3k)=  -9k

-40+48-9= -1

E=  

i	j	k	i	j
5	8	3	5	8
-8	6	-3	-8	6

5	8	3	5	8
-8	6	-3	-8	6

i	j	k
30	-24	24
-15	-64	-18
15	-88	6

En la suma de vectores, se suma cada valor de cada vector según su variante, para el final obtener el resultado de i, j, k. Al igual con la resta solo que hay que verificar el cambio de signo.

El producto punto se saca multiplicando cada variante, como por ejemplo (5i) (8i), y al final de la multiplicación se suma todo para obtener un resultado final.

En el producto cruz utilizaremos el método de matriz.

Examen 3ra Unidad.

Evelyn Perez Contreras 

Número de lista 8. 

Ejercicio 4

Ejercicio 3

Puntos notables en un Triángulo

Puntos notables de un Triangulo

Circuncentro

Cualquier punto de la mediatriz de un lado de un triángulo equidista de los vértices que definen dicho lado. Luego si llamamos O al punto de intersección de las mediatrices de los lados AB y BC, por la propiedad anterior, el punto O equidista de los vértices A y B (por estar en la mediatriz de AB) y de los vértices B y C (por estar en la mediatriz de BC). Luego equidista de A, B y C .

Al equidistar de los tres vértices del triángulo, en particular, equidista de A y C, lo que demuestra que también estará en la mediatriz del lado AC y, además, será el centro de una circunferencia que pasa por los tres vértices del triángulo.

Las tres mediatrices de un triángulo se cortan en un ÚNICO punto, que denotaremos por O, y que recibe el nombre de CIRCUNCENTRO.

El punto de corte de las tres mediatrices es el CENTRO de un circunferencia que pasa por los tres vértices del triángulo, que llamaremos circunferencia circunscrita.

Observa el circuncentro en los casos de que el triángulo sea rectángulo, acutángulo u obtusángulo, respectivamente.

Propiedad 1:

A la vista de los dibujos anteriores, podemos enunciar la siguiente propiedad:

"El Circuncentro de un triángulo rectángulo es el punto medio de la hipotenusa"
"El Circuncentro de un triángulo acutángulo está en el interior del triángulo"
"El Circuncentro de un triángulo obtusángulo está en el exterior del triángulo"

Ejercicio 1:

1.       Con ayuda de una regla y compás:

2.       Dibuja un triángulo acutángulo cualquiera.

3.       Dibuja dos de sus mediatrices (las que tú quieras).

4.       Señala el punto de intersección de ambas.

5.       Traza la circunferencia con centro en ese punto y radio la distancia al vértice A.

6.       Comprueba que dicha circunferencia pasa por los vértices B y C.

7.       Repite el ejercicio anterior con un triángulo rectángulo.

8.       Repite el ejercicio anterior con un triángulo obtusángulo.

9.       Comprueba que se ha verificado la propiedad 11 en cada uno de los triángulos que has dibujado.

Incentro

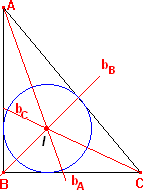
Cualquier punto de la bisectriz de un ángulo de un triángulo equidista de los lados que definen dicho ángulo. Luego si llamamos I al punto de intersección de las bisectrices de los ángulos A y B, por la propiedad anterior, el punto I equidista de los lados AB y AC (por estar en la bisectriz de A) y de los lados AB y BC (por estar en la bisectriz de B). Luego equidista de los lados AB, BC y CA.

Al equidistar de los tres lados del triángulo, en particular, equidista de CA y CB, lo que demuestra que también estará en la bisectriz del ángulo C y, además, será el centro de una circunferencia que es tangente a los tres lados del triángulo.

Las tres bisectrices de un triángulo se cortan en un ÚNICO punto, que denotaremos por I, y que recibe el nombre de INCENTRO.

El punto de corte de las tres bisectrices es el CENTRO de un circunferencia tangente a los tres lados del triángulo, que llamaremos circunferencia inscrita.

Observa el incentro en los casos de que el triángulo sea rectángulo, acutángulo u obtusángulo, respectivamente.

Propiedad 2:

"El incentro de un triángulo cualquiera está siempre en el interior del triángulo"

Ejercicio 2:

1.       Con ayuda de una regla y compás:

2.       Dibuja un triángulo acutángulo cualquiera.

3.       Dibuja dos de sus bisectrices (las que tú quieras).

4.       Señala el punto de intersección de ambas.

5.       Traza la circunferencia con centro en ese punto y tangente al lado AB.

6.       Comprueba que dicha circunferencia también es tangente a los otros dos lados.

7.       Repite el ejercicio anterior con un triángulo rectángulo.

8.       Repite el ejercicio anterior con un triángulo obtusángulo.

9.       En cada uno de los triángulos que has dibujado, comprueba que el incentro está siempre en el interior del triángulo.

Baricentro

Las tres medianas de un triángulo, al igual que ocurría con las mediatrices y bisectrices, se cortan en un ÚNICO punto, que llamaremos BARICENTRO.

Como puedes ver en los dibujos anteriores, no hay diferencias significativas en la situación del baricentro, dependiendo del tipo de triángulo (rectángulo, acutángulo u obtusángulo). En cualquier triángulo, el baricentro siempre es interior al mismo, más aún, es el centro de gravedad del triángulo y se denotará por G.

Propiedad 3:

"El baricentro de un triángulo, es un punto interior al mismo, que dista el doble de cada vértice que del punto medio de su lado opuesto"

Sin entrar en la demostración, que se sale fuera de los objetivos de este curso, sí que lo veremos gráficamente en los tres casos: triángulos rectángulos, acutángulos y obtusángulos, respectivamente.

Se han denotado por A', B', C', los puntos medios de los lados "a "=BC, "b "=AC y "c "=AB, respectivamente, y se ha señalado el punto medio de las distancias del baricentro a cada vértice, mediante un punto negro sin etiquetar.

A la vista del anterior, se observa que:

GA = 2GA'	(la distancia de Baricentro al vértice A es igual a dos veces la distancia del baricentro al punto medio del lado "a"=BC)
GB = 2GB'	(la distancia de Baricentro al vértice B es igual a dos veces la distancia del baricentro al punto medio del lado "b"=AC )
GC = 2GC'	(la distancia de Baricentro al vértice C es igual a dos veces la distancia del baricentro al punto medio del lado "c"=AB )

Ejercicio 3:

1.       Con ayuda de regla y compás:

2.       Dibuja un triángulo cualquiera.

3.       Traza geométricamente dos de las medianas.

4.       Señala el punto donde se han cortado ¿cómo se llama ese punto?.

5.       Traza la tercera mediana y comprueba que pasa por dicho punto.

6.       Con el compás:

7.       Toma la medida del baricentro al punto medio del lado AB.

8.       Comprueba que puedes llevar esta medida, sobre la mediana, DOS veces desde el baricentro hasta el vértice C.

9.       Repite el apartado anterior con las otras dos medianas.

Ortocentro

Consideremos un triángulo de vértices A', B' y C'. Ya demostramos que las mediatrices de dicho triángulo se cortaban en un único punto, llamado circuncentro.

Ahora bien, si llamas A, B y C a los puntos medios de los lados B'C', A'C' y A’B’, respectivamente, y consideras el triángulo ABC. Podemos comprobar lo siguiente:

Los lados de los triángulos ABC y A'B'C', son respectivamente paralelos.

La mediatriz del lado A'B' es la perpendicular a A'B' que pasa por su punto medio (C), luego será también perpendicular a AB (por ser paralelo a A'B'). Así pues, considerando el triángulo ABC, dicha recta es perpendicular a AB pasando el vértice C, o lo que es lo mismo, es la altura del triángulo ABC respecto del lado AB.

Análogo razonamiento nos lleva a deducir que la mediatriz del lado A'C' del triángulo A'B'C', coincide con la altura del triángulo ABC respecto del lado AC. Y, la mediatriz del lado B'C' del triángulo A'B'C', coincide con la altura del triángulo ABC respecto del lado BC.

Las alturas del triángulo ABC, son las mediatrices del A'B'C', y como las mediatrices de cualquier triángulo se cortaban en un único punto, podemos deducir:

Las alturas de cualquier triángulo se cortan en un único punto, que llamaremos ORTOCENTRO, y que denotaremos por H.

Además, el ortocentro de este triángulo coincide con el circuncentro de un triángulo semejante al dado, y que tiene los vértices del primero como puntos medios de sus lados.

Propiedad 4:

"El Ortocentro de un triángulo rectángulo es el vértice correspondiente al ángulo recto"
"El Ortocentro de un triángulo acutángulo está en el interior del triángulo"
"El Ortocentro de un triángulo obtusángulo está en el exterior del triángulo"

Ejercicio 4:

1.      Con ayuda de una regla y compás::

2.      Dibuja un triángulo acutángulo cualquiera ABC.

3.      Dibuja dos de sus alturas, tal y como se explicó en la construcción geométrica de la altura.

4.      Señala el punto de intersección de ambas. ¿cómo se llama dicho punto?

5.      ¿El ortocentro está dentro o fuera del triángulo?

6.      Con ayuda de una regla y compás:

7.      Dibuja un triángulo obtusángulo cualquiera ABC.

8.      Dibuja otro triángulo A'B'C' que tenga los vértices A, B, y C, como puntos medios de sus lados.

9.      Calcula dos mediatrices del triángulo A'B'C', tal y como se explicó en la construcción geométrica de la mediatriz.

10.  Señala el punto de intersección de ambas mediatrices. ¿cómo se llama dicho con respecto al triángulo ABC?

11.  ¿El ortocentro está dentro o fuera del triángulo?

Propiedad 5:

1.      El Ortocentro, Baricentro y Circuncentro están siempre ALINEADOS.

2.      El baricentro está ENTRE el ortocentro y circuncentro.

3.      La distancia del baricentro al circuncentro es la mitad que la distancia del baricentro al ortocentro.

Además, la recta que pasa por los tres puntos citados (Ortocentro, Baricentro y Circuncentro) se llama RECTA 

Ejercicio 5:

1.       Con ayuda de regla y compás:

2.       Dibuja un triángulo acutángulo cualquiera.

3.       Traza geométricamente el Ortocentro, Baricentro y circuncentro.

4.       Dibuja la Recta de Euler.

5.       Con el compás:

6.       Toma la medida del baricentro al circuncentro.

7.       Comprueba que puedes llevar esta medida, sobre la recta de Euler, DOS veces desde el baricentro hasta el ortocentro.

8.       Repite los apartados 1 y 2 con un triángulo rectángulo.

9.       Repite los apartados 1 y 2 con un triángulo obtusángulo.